Rで解析：カイ二乗検定とフィッシャーの正確確率検定のコマンド紹介

カイ二乗検定とフィッシャーの正確確率検定は2つのカテゴリー、例えば「甘いものが好きか？辛いものが好きか？をYes, Noで答えたアンケート」等でよく使われる手法だと思います。

なお、カイ二乗検定のコマンドchisq.testは初期設定でイェーツの補正が設定されていますのでご注意を。

また、フィッシャーの正確確率検定はいくつかのセルの期待頻度が4以下の分割表の解析で使用されます。

chisq.testで「カイ自乗近似は不正確かもしれません」と表示されたら使用してみてください。

コマンド

各コマンドの詳細オプションはヘルプを確認してください。

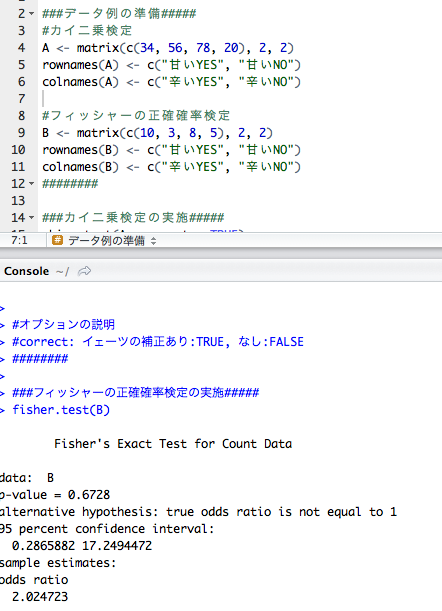
###データ例の準備#####
#カイ二乗検定
A <- matrix(c(34, 56, 78, 20), 2, 2)
rownames(A) <- c("甘いYES", "甘いNO")
colnames(A) <- c("辛いYES", "辛いNO")

#フィッシャーの正確確率検定
B <- matrix(c(10, 3, 8, 5), 2, 2)
rownames(B) <- c("甘いYES", "甘いNO")
colnames(B) <- c("辛いYES", "辛いNO")
########

###カイ二乗検定の実施#####
chisq.test(A, correct = TRUE)

Pearson's Chi-squared test with Yates' continuity correction

data:  A
X-squared = 32.3455, df = 1, p-value = 1.291e-08

#オプションの説明
#correct: イェーツの補正あり:TRUE, なし:FALSE
########

###フィッシャーの正確確率検定の実施#####
fisher.test(B)

Fisher's Exact Test for Count Data

data:  B
p-value = 0.6728
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  0.2865882 17.2494472
sample estimates:
odds ratio 
  2.024723 
########

少しでも、あなたの解析が楽になりますように！！