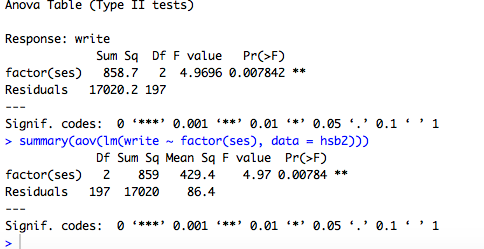
一元配置分散分析と二元配置分散分析のコードの例です。UCLAのページが参考になります。
CHOOSING THE CORRECT STATISTICAL TEST IN SAS, STATA, SPSS AND R http://www.ats.ucla.edu/stat/mult_pkg/whatstat/
コードの紹介
理論は他のサイトを参考にしてください。下記コードでSPSSと同じ結果を算出することができます。
#一元配置分散分析
hsb2 <- read.table("https://stats.oarc.ucla.edu/stat/data/hsb2.csv", sep = ",", header = T)
library(car)
Anova(lm(write ~ factor(ses), data = hsb2), type = 2)
#Anova Table (Type II tests)
#Response: write
#Sum Sq Df F value Pr(>F)
#factor(ses) 858.7 2 4.9696 0.007842 **
# Residuals 17020.2 197
#---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(aov(lm(write ~ factor(ses), data = hsb2)))
#Df Sum Sq Mean Sq F value Pr(>F)
#factor(ses) 2 859 429.4 4.97 0.00784 **
# Residuals 197 17020 86.4
#---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
########################################
#二元配置分散分析
exer <- read.csv("https://stats.oarc.ucla.edu/stat/data/exer.csv")
exer <- within(exer, {
diet <- factor(diet)
exertype <- factor(exertype)
time <- factor(time)
id <- factor(id)
})
exertype.aov <- aov(pulse ~ exertype * time + Error(id), data = exer)
summary(exertype.aov)
#Error: id
#Df Sum Sq Mean Sq F value Pr(>F)
#exertype 2 8326 4163 27 3.62e-07 ***
# Residuals 27 4163 154
#---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#Error: Within
#Df Sum Sq Mean Sq F value Pr(>F)
#time 2 2067 1033.3 23.54 4.45e-08 ***
# exertype:time 4 2723 680.8 15.51 1.65e-08 ***
# Residuals 54 2370 43.9
#---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1少しでも、あなたのウェブや実験の解析が楽になりますように!!